Disclaimer: This example is taken from a reference titled ‘R In A Nutshell’ by Joseph A. Adler
In Machine Learning (ML), Regression is a supervised learning technique used to observe a correlation between variables (features/predictor) and to predict the continuous output (label/response) based on one or more variables. It is mainly used in prediction, forecasting, time-series modeling and determining the causal-effect relationship between variables.
One of the simplest technique of regression analysis is Linear Regression.
A linear regression assumes that there is a linear relationship between the response (label) variable and the predictor (features) variable
– R In A Nutshell, Joseph A. Adler
To study how linear regression works, let’s look at an example taken from the reference book. In this example, we are going to analyze a sample dataset collected on baseball teams scores.
First, load the lattice package.
library(lattice)Next, load the dataset.
load("team.batting.00to08.rda")I like to check the dimension of the dataset before I proceed, so that I have an idea of how big the dataset that I am going to work on.
> dim(team.batting.00to08)
[1] 270 13Then, have a peek at the sample data in the dataset.
> head(team.batting.00to08)
teamID yearID runs singles doubles triples homeruns walks stolenbases
1 ANA 2000 864 995 309 34 236 608 93
2 BAL 2000 794 992 310 22 184 558 126
3 BOS 2000 792 988 316 32 167 611 43
4 CHA 2000 978 1041 325 33 216 591 119
5 CLE 2000 950 1078 310 30 221 685 113
6 DET 2000 823 1028 307 41 177 562 83
caughtstealing hitbypitch sacrificeflies atbats
1 52 47 43 5628
2 65 49 54 5549
3 30 42 48 5630
4 42 53 61 5646
5 34 51 52 5683
6 38 43 49 5644Ok, now we are ready to begin our analysis. We are going to see how different features (metrics) such as singles, doubles, triples, homeruns, walks, stolenbases, caughtstealing, hitbypitch, sacrificeflies and atbats are related to the number of runs for each baseball team.
Let’s start with this;
runs~singles+doubles+triples+homeruns+walks+stolenbases
+caughtstealing+hitbypitch+sacrificeflies+atbatsA linear regression model suggested that;
y = I + C1x1 + C2x2 + C3x3 + ...
where I is the Interceptor and C is the Coefficient, while y is the response and x is the predictors.Before we train the data, we are going to transform it into a data frame first.
attach(team.batting.00to08)
forplot <- make.groups(
singles = data.frame(value=singles, teamID,yearID,runs),
doubles = data.frame(value=doubles, teamID,yearID,runs),
triples = data.frame(value=triples, teamID,yearID,runs),
homeruns = data.frame(value=homeruns, teamID,yearID,runs),
walks = data.frame(value=walks, teamID,yearID,runs),
stolenbases = data.frame(value=stolenbases, teamID,yearID,runs),
caughtstealing = data.frame(value=caughtstealing,teamID,yearID,runs),
hitbypitch = data.frame(value=hitbypitch, teamID,yearID,runs),
sacrificeflies = data.frame(value=sacrificeflies,teamID,yearID,runs)
)
detach(team.batting.00to08)Then, plot it so that we can observe the distributions of the data.
xyplot(runs~value|which, data=forplot,
scales=list(relation="free"), pch=19, cex=.2,
strip=strip.custom(strip.levels=TRUE,
horizontal=TRUE,
par.strip.text=list(cex=.8)))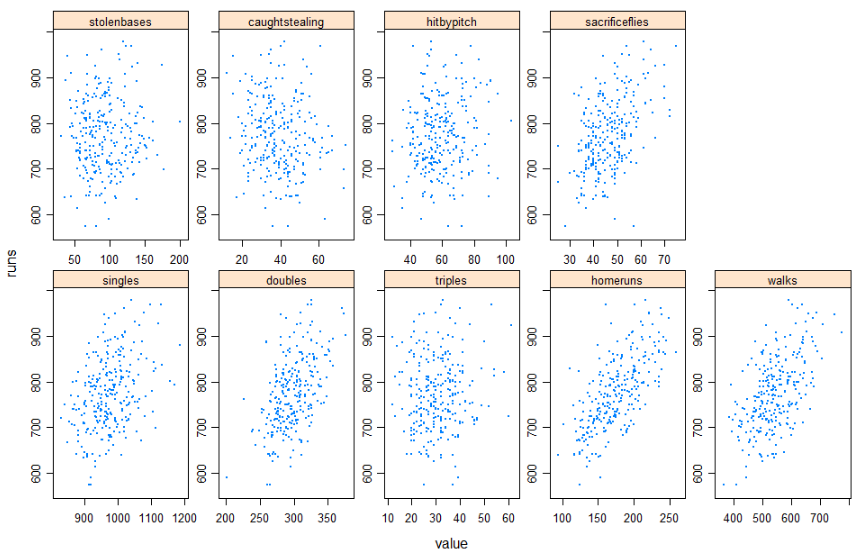
Based on the plot, we can see that as predicted, teams that hit a lot of homeruns definitely score more runs. Eventually, teams that walks also able to score more runs as well. Interesting.
Next, training the data so that we can check out our hypotheses about the relationship between the features (singles, doubles, homeruns, etc.) and the number of runs for each team. For training, we are going to use the lm function.
runs.mdl <- lm(formula=runs~singles+doubles+triples+homeruns+walks+hitbypitch+sacrificeflies+stolenbases+caughtstealing, data=team.batting.00to08)View the model returned.
> runs.mdl
Call:
lm(formula = runs ~ singles + doubles + triples + homeruns +
walks + hitbypitch + sacrificeflies + stolenbases + caughtstealing,
data = team.batting.00to08)
Coefficients:
(Intercept) singles doubles triples homeruns
-507.16020 0.56705 0.69110 1.15836 1.47439
walks hitbypitch sacrificeflies stolenbases caughtstealing
0.30118 0.37750 0.87218 0.04369 -0.01533 Use the summary function to get the summary of the linear model object.
> summary(runs.mdl)
Call:
lm(formula = runs ~ singles + doubles + triples + homeruns +
walks + hitbypitch + sacrificeflies + stolenbases + caughtstealing,
data = team.batting.00to08)
Residuals:
Min 1Q Median 3Q Max
-71.902 -11.828 -0.419 14.658 61.874
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -507.16020 32.34834 -15.678 < 2e-16 ***
singles 0.56705 0.02601 21.801 < 2e-16 ***
doubles 0.69110 0.05922 11.670 < 2e-16 ***
triples 1.15836 0.17309 6.692 1.34e-10 ***
homeruns 1.47439 0.05081 29.015 < 2e-16 ***
walks 0.30118 0.02309 13.041 < 2e-16 ***
hitbypitch 0.37750 0.11006 3.430 0.000702 ***
sacrificeflies 0.87218 0.19179 4.548 8.33e-06 ***
stolenbases 0.04369 0.05951 0.734 0.463487
caughtstealing -0.01533 0.15550 -0.099 0.921530
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 23.21 on 260 degrees of freedom
Multiple R-squared: 0.9144, Adjusted R-squared: 0.9114
F-statistic: 308.6 on 9 and 260 DF, p-value: < 2.2e-16Here’s the ANOVA statistics for the model.
> anova(runs.mdl)
Analysis of Variance Table
Response: runs
Df Sum Sq Mean Sq F value Pr(>F)
singles 1 215755 215755 400.4655 < 2.2e-16 ***
doubles 1 356588 356588 661.8680 < 2.2e-16 ***
triples 1 237 237 0.4403 0.507565
homeruns 1 790051 790051 1466.4256 < 2.2e-16 ***
walks 1 114377 114377 212.2971 < 2.2e-16 ***
hitbypitch 1 7396 7396 13.7286 0.000258 ***
sacrificeflies 1 11726 11726 21.7643 4.938e-06 ***
stolenbases 1 357 357 0.6632 0.416165
caughtstealing 1 5 5 0.0097 0.921530
Residuals 260 140078 539
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1Based on the statistics, it appears that triples, stolenbases and caughtstealing are not significant to the number of runs scored by each team.
Click here to download the dataset.