Disclaimer: This example is taken from a reference titled ‘R In A Nutshell’ by Joseph A. Adler
Classification is another type of supervised learning in Machine Learning (ML). Classification is a process of categorizing a given set of data into classes. The classes are also known as target, label or categories (thus categorization).
Examples of classification problem includes predicting weather a particular patient is diabetic or not based on their collected medical data/records, or to scan if incoming email is spam or not based on a list of filtered keywords.
Today, we are going to look at an example of a classification problem taken from the reference book. In this example, we will apply a logistic regression model.
Logistic regression is a statistical model that in its basic form uses a logistic function to model a binary dependent variable, although many more complex extensions exists. In regression analysis, logistic regression is estimating the parameters of a logistic model (a form of binary regression). Mathematically, a binary logistic model has a dependent variable with two possible values, such as pass/fail which is represented by an indicator label, where the two values are labeled “0” and “1”.
– Wikipedia
The sample dataset that we will use is a field goal dataset. Each time a kicker attempts a field goal (i.e.. kick), there is a chance that the goal will be successful, and a chance that it will fail. The probability varies according to distance; any attempts closer to the goal posts are more likely to be successful.
As usual before we start, load the lattice package.
library(lattice)Next, load the dataset.
load("field.goals.rda")Check the dimension of the dataset.
> dim(field.goals)
[1] 982 10Call head() on the dataset to get an idea how the data looks like.
> head(field.goals)
home.team week qtr away.team offense defense play.type player yards stadium.type
1 ARI 14 3 WAS ARI WAS FG good 1-N.Rackers 20 Out
2 ARI 2 4 STL ARI STL FG good 1-N.Rackers 35 Out
3 ARI 7 3 TEN ARI TEN FG good 1-N.Rackers 24 Out
4 ARI 12 2 JAC JAC ARI FG good 10-J.Scobee 30 Out
5 ARI 2 3 STL ARI STL FG good 1-N.Rackers 48 Out
6 ARI 7 4 TEN TEN ARI FG aborted 15-C.Hentrich 33 OutLet’s transform the dataset and create a new binary variable for field goals that are either good or bad.
field.goals.forlr <- transform(field.goals, good=as.factor(ifelse(play.type=="FG good","good","bad")))View the transformed dataset. A new column “good” has been added to the dataset.
> head(field.goals.forlr)
home.team week qtr away.team offense defense play.type player yards stadium.type good
1 ARI 14 3 WAS ARI WAS FG good 1-N.Rackers 20 Out good
2 ARI 2 4 STL ARI STL FG good 1-N.Rackers 35 Out good
3 ARI 7 3 TEN ARI TEN FG good 1-N.Rackers 24 Out good
4 ARI 12 2 JAC JAC ARI FG good 10-J.Scobee 30 Out good
5 ARI 2 3 STL ARI STL FG good 1-N.Rackers 48 Out good
6 ARI 7 4 TEN TEN ARI FG aborted 15-C.Hentrich 33 Out badWe are going to plot the dataset to have a better understanding on the relationship between field goals and distance (column: yards). Before that, let’s tabulate the dataset.
> field.goals.table <- table(field.goals.forlr$good, field.goals.forlr$yards)
> field.goals.table
18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62
bad 0 0 1 1 1 1 0 0 0 3 5 5 2 6 7 5 3 0 4 3 11 6 7 5 6 11 5 9 12 11 10 9 5 8 11 10 3 1 2 1 1 1 1 1 1
good 1 12 24 28 24 29 30 18 27 22 26 32 22 21 30 31 21 25 20 23 29 35 27 32 21 15 24 16 15 26 18 14 11 9 12 10 2 1 3 0 1 0 0 0 0The top row is the yards. Followed by the total bad and good field goals respectively.
Now, we plot the results.
plot(colnames(field.goals.table), field.goals.table["good",]/ (field.goals.table["bad",] +field.goals.table["good",]), xlab="Distance (Yards)", ylab="Percent Good")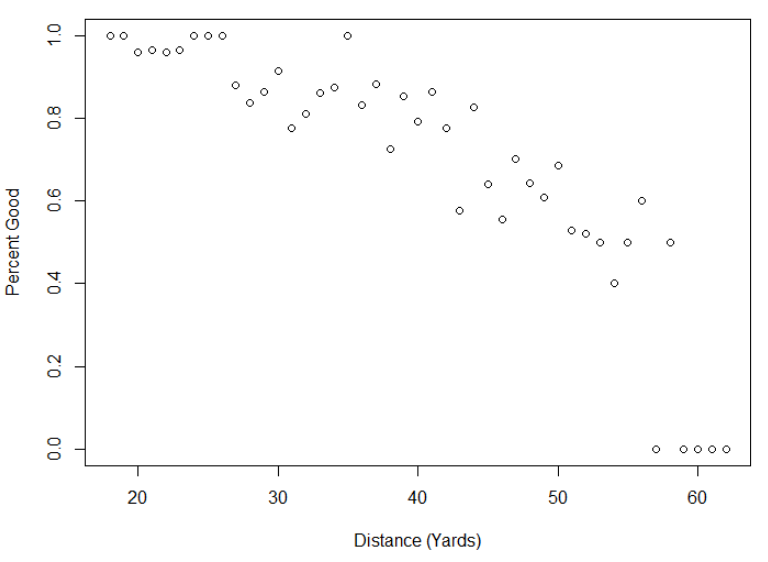
We can see from the plot that there is a linear relationship between the field goals and the distance, though with some outliers at the right bottom. It clearly shows that as the distance increases, the number of successful field goals decreases. In other words, the closer the player to the goal posts, the higher the chances of scoring a goal.
To model the probability of a successful field goal using a logistic regression, call glm() function.
> field.goals.mdl <- glm(formula=good~yards, data=field.goals.forlr, family="binomial")
> field.goals.mdl
Call: glm(formula = good ~ yards, family = "binomial", data = field.goals.forlr)
Coefficients:
(Intercept) yards
5.17886 -0.09726
Degrees of Freedom: 981 Total (i.e. Null); 980 Residual
Null Deviance: 978.9
Residual Deviance: 861.2 AIC: 865.2The call the summary function to get a more detailed results. We can see the the coefficients for yards is a negative value, which kind of concurred to our earlier hyphotheses i.e. the closer the player to the goal posts, the higher the chances of having a successful field goal.
> summary(field.goals.mdl)
Call:
glm(formula = good ~ yards, family = "binomial", data = field.goals.forlr)
Deviance Residuals:
Min 1Q Median 3Q Max
-2.5582 0.2916 0.4664 0.6978 1.3789
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 5.178856 0.416201 12.443 <2e-16 ***
yards -0.097261 0.009892 -9.832 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 978.90 on 981 degrees of freedom
Residual deviance: 861.22 on 980 degrees of freedom
AIC: 865.22
Number of Fisher Scoring iterations: 5Finally, plot the results to see how this model fits the data, and we are also going to draw a line to show the trends.
> plot(colnames(field.goals.table), field.goals.table["good",]/ (field.goals.table["bad",] + field.goals.table["good",]), xlab="Distance (Yards)", ylab="Percent Good")
> # add a line to chart
> fg.prob <- function(y) {
+ eta <- 5.178856 + -0.097261 * y;
+ 1 / (1 + exp(-eta))
+ }
> lines(15:65,fg.prob(15:65),new=TRUE)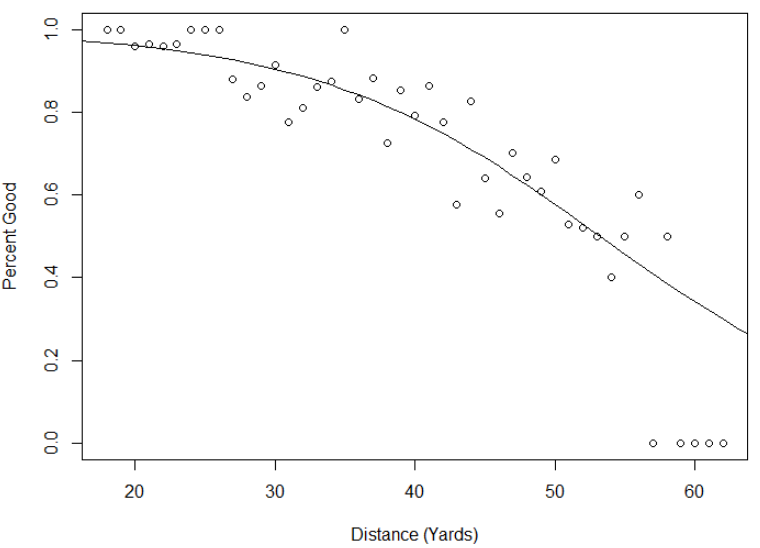
As expected from the statistics above, the model looks like it fits the data reasonably well.
Click here to download the dataset.